Where do we want to go from here?
In a previous post, I tried (and from the feedback I got, somehow succeeded) to introduce the beauty of developing extensions to the core capabilities of ANSYS by means of APDL Math commands.
Now, that was merely an introduction, using but the most simple physics (linear thermal model) and solver (modal thermal). There is of course much more to be expected from such general capabilities as matrix manipulation, and since they are meant to address some “unconventional” needs, it would hardly make sense to go on and try finding the additional capability “everybody was waiting for”.
Hence, I am going to follow the track I started so far, and resume my journey into the wonders of APDL Math with the natural extension of modal analysis that is, harmonic analysis. This might be directly useful to a few readers, and hopefully will be an incentive for users to use the existing solvers for answering their own needs.
Thermal Harmonic Analysis at a Glance
Thermal harmonic analysis is so scarcely used that, as of May 2018, even Google had not heard about it. No, seriously, not a single match. Gulp. But don’t panic, it is nothing esoteric, really. The concept was introduced as early as the 1960’s (see ref [1]), and is used under one form or the other every time it is necessary to design a system with high immunity against thermal disturbances. Actually, you would encounter it under one form or the other whenever stringent dimensional stability – hence thermal stability – is required.
Specifically, it can provide quantitative answers to crucial design questions:
- Q: What will be the net fraction of external temperature fluctuations that will propagate into my system?
- A: Compute Thermal Transmissibility
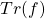between the “noisy” and the “quiet” side. Once obtained, the temperature fluctuations Power Spectral Density (PSD) on the quiet side will be given by the usual relationship for linear systems (i.e. 
=
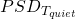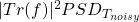). From this, estimating the RMS temperature fluctuation on the quiet side is straightforward. Even more importantly, it also grants knowledge to the temperature drift rate and its Allan Variance, that in turn allows one to estimate the maximum allowable duration for an experiment .
- Q: Assuming stability demands are not fulfilled with a passive design: Can I develop an “open loop” frequency response, so as to decide where to put sensors and actuators (heaters) for an active thermal control system?
- A: Thermal Harmonic response will provide just what you need, that is, the complex frequency response, giving access to gain and phase. This in turn can be used at the system level to decide on the most appropriate sensors / actuators / controller logic configuration
- Q: Assuming I am working with a purely optical system, how deleterious will short duration fluctuations of light beam?
- A: Compute the thermal harmonic response of the system at the beam oscillation frequency (or frequencies). The thermal solution can then be used to estimate the severity of thermally induced distortions (either variation of the material’s refractive index with temperature or thermoelastic expansion) on the final optical performance.
- Q: Assuming I am working with a structural part submitted to complex thermal loading (i.e. randomly distributed, time and space wise), how can I estimate thermal fatigue?
- A: Thermal fatigue effects can be effectively captured, since Thermal Harmonic Analysis gives access to (complex) structural temperature fields, with no restriction on the analysis bandwidth. These temperature fields can be used to estimate mechanical stress response patterns, just like the ones produced by a conventional random vibration analysis.
Especially when both thermal and mechanical effects are involved, efficiency is of paramount importance, because of two technical hurdles acting in conjunction: Firstly, since mechanical stress is the final quantity of interest, spatial resolution (mesh size) becomes non-negotiable. And secondly, the loading itself spans orders of magnitudes in correlation length and frequencies, hence the model cannot be strictly restricted to the area of interest without introducing severe bias in the results. Running long transient analyses of a finely meshed model with small time steps is exactly what one should avoid doing.
Even if your application does not involve thermal mechanical phenomena, as soon as linear behavior can be granted, you might want to consider harmonic analysis. Working in the frequency domain not only allows for improved insight but it also drastically reduces the computational burden.