Working wonders with APDL Math – Ep 01 : Thermal Modal Analysis

As Times Goes By

Do you remember the moment you first heard about ANSYS introducing APDL Math?

I, for one, do, and I have a vivid memory of thinking “Wow, that can be a powerful tool, I’m dead sure it won’t be long before an opportunity arises and I’ll start developing pretty useful procedures and tools”. Well, that was half a decade ago, and to my great shame, nothing quite like that has happened so far. Reasons for this are obvious and probably the same for most of us:  lack of time and energy to learn yet another set of commands, fear of the ever present risk of developing procedures that are eventually rejected as nonstandard use of the software and therefore error-prone (those of you working under quality assurance, raise your hand!), anxiety of working directly under the hood on real projects with little means to double check your results, to name a few.

That said, finally an opportunity presented itself, and before I knew it, I was up and running with APDL Math. The objective of this article is to showcase some simple yet insightful applications and hopefully remove the prevention one can have regarding using these additional capabilities.

For the sake of demonstration, I will begin with a somewhat uncommon analysis tool that should nevertheless ring a bell for most of you, that is: modal analysis (and yes, the pun is intended). You may wonder what is the purpose of using APDL Math to perform a task that is a standard ANSYS capability since say revision 2.0, 40 years ago? But wait, did I mention that by modal analysis, I mean thermal modal Analysis?

Thermal Modal Analysis at a Glance

Although scarcely used, thermal modal analysis is both an analysis and a design validation tool, mostly used in the field of precision engineering and or optomechanics. Specifically, it can serve a number of purposes such as in the following Q&A:

Q: Will my system settle fast enough to fulfill design requirements?

A: Compute the system Thermal Time Constants

Q: Where should I place sensors to get information rich / robust measurements?

A: Compute Thermal modes and place your sensors away from large thermal gradients

Q: Can I develop a reduced model to solve large transient thermal mechanical problems?

A: Working on a modal basis rather than with the full problem allows for the construction of such reduced model effectively converting a high-order coupled system to a low order, uncoupled set of equations.

Q: How to develop a reduced order state-space matrices representation of my thermal system (equivalent to SPMWRITE command)?

A: Modal analysis provides every result needed to build those matrices directly within ANSYS.

Although you might only be vaguely familiar with many or all of those topics, the idea behind this article is really to show that APDL Math does exactly what you need it to do: allow the user to efficiently address specific needs, with a minimal amount of additional work. Minimal? Let’s see what it looks like in reality, and you will soon enough be in a position to make your own opinion on the matter.

 Thermal Modal Analysis using APDL Math

To begin with, it is worth underlining the similarities and differences between structural (vibration) modes and thermal modes. Mathematically, both look very much the same, i.e. modes are solutions of the dynamics equation in the absence of forcing (external) term:

Domain	Equation solved	Terms Explained
Structural
Thermal

Now, the fundamental difference is that the eigenvalues have completely different physical interpretations:

• in the structural case, 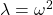, i.e. the eigenvalue is the square of the modal circular frequency
• in the thermal case, 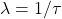, i.e. the eigenvalue is the inverse of the modal time constant

This is a direct consequence of the fact that dynamical systems are 2^nd order systems, whereas thermal systems are 1^st order systems. While after being disturbed the former will oscillate around its equilibrium position, the latter will return to its initial state via exponential decay. Mind you, there is no such thing as thermal resonances!

No big deal, right? Hence, the APDL Math code for Thermal Modal Analysis should be a straightforward adaption of the original. As it turns out, the modifications are quite small. Below is a table comparing input codes to perform both type of analyses, using APDL Math.

Structural	Thermal
! Setup Model …   ! Make ONE dummy transient solve to write stiffness and mass matrices to .FULL file /SOLU ANTYPE,TRANSIENT TIME,1 WRFULL,1 SOLVE       ! Get Stiffness and Mass *SMAT,MatK,D,IMPORT,FULL,,STIFF *SMAT,MatM,D,IMPORT,FULL,,MASS                       ! Eigenvalue Extraction Antype,MODAL modopt,Lanb,NRM,0,Fmax *EIGEN,MatK,MatM,,EiV,MatPhi   ! No need to convert eigenvalues to frequencies, ANSYS does it automatically     ! Done !	! Setup Model … ! Make TWO dummy transient solve to separately write conductivity and capacitances matrices to .FULL file /SOLU ANTYPE,TRANSIENT TIME,1 NSUB,1,1,1 TINTP,,,,1 WRFULL,1 ! Zero out capacitance terms … SOLVE ! Get Conductivity Matrice *SMAT,MatK,D,IMPORT,FULL, Jobname.full,STIFF ! Restore capacitance and zero out conductivity terms … SOLVE ! Get Capacitance Matrice *SMAT,MatC,D,IMPORT,FULL,,STIFF   ! Eigenvalue Extraction Antype,MODAL modopt,Lanb,NRM,,0,1/(2*PI*SQRT(Tmin)) *EIGEN,MatK,MatC,,EiV,MatPhi   ! Convert Eigenvalues for Frequency to Thermal time Constants *do,i,1,EiV_rowDim Eiv(i)=1/(2*PI*Eiv(i))**2 *enddo   ! Done !

The only data requested from the users is the number of requested modes (NRM) as well as the upper frequency (or for that matter, the shortest time constant of interest). Also, note that in the thermal case, one needs to perform two separate dummy analyses to store the conductivity and capacitance matrices, since internally those are merged into an equivalent stiffness (conductivity) matrix .

(Note: Theta is the 1st order transient integration parameter and defaults to 1.0, see the TINTP command for instance).

If you are familiar with APDL, some important differences are apparent here:

Resultig eigenvalues are stored in a vector (EiV) and eigenvectors a matrix (MatPhi), which need not be declared but are created when executing the *EIGEN command (no *DIM required)

For each APDL Math entity, ANSYS automatically maintains variables named Param_rowDim and Param_colDim, hence removing the burden to keep track of dimensions.