Tag: Model Reduction

Data reduction for real-world applications

In the previous post of this series (here: Working Wonders with ADPL Math – Ep 03: Data Reduction Fundamentals), we have seen that using a bunch of APDL Math commands, it is possible to reduce large volume of data (i.e. snaphots) very efficiently. Now, data reduction method like POD is obviously attractive but reducing results file size is rarely a major concern. More often than not, obtaining simulation results with minimal computational effort is what we are looking for.

So, how can we use POD for practical situations? There are a bunch of possibilities, that we will explore in the upcoming episode of this series. Here, we will begin with the simplest and straightforward situation one could think of: thermal elastic simulations.

Thermal-elastic simulations from data reduction perspective

There are many instances where one needs to efficiently execute thermal-elastic situations. From a fatigue point of view, for example, it is useful to run analyses with numerous realistic transients (possibly using actual records) rather than a single, penalizing transient, with generally huge, but unknown built-in safety margins.

In such a situation, one will generally solve the problem sequentially:

• First thermally, in the time-domain, possibly accounting for non-linear phenomena and/or time-dependent characteristics. Here, the emphasis needs to be put on capturing temperature elevation as well as gradients which are drivers of flexural stresses.
• The resulting temperature snapshots are then feed into a structural model, where inertia effect are neglected. Hence, static structural solutions are needed.

To emphasize, capturing the exact temperature or stress time-histories is not mandatory: the figure of merit here will be stress range, i.e. extreme values.

Now, the regular approach would be to solve in the time domain for the temperature distribution in the structure T(x,t) at a series of instants t₁..t_n. From this, a series of n structural solutions would be performed, producing the structural displacement U(x,t), and derived quantities such as stress/strain. Note that, the structural displacements could be estimated “on the fly”, as structural displacement at time “t” obviously doesn’t depend on past or future values.

Alternatively, the POD approach would consist in:

1. Evaluating the temperature distributions at all time points, i.e. the snapshot matrix ().
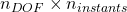2. Compressing those snapshots using SVD method: this produces a set of nodal amplitudes (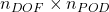) and POD vectors amplitudes()
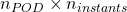3. Evaluate the individual structural response for each of the thermal POD vectors .
4. Combine the individual structural responses to obtain the physical response at all locations and time points.

The expected computational gain is clearly related to the ratio between the number of time points and that of the required POD vectors, and we should expect the solution time reduction to be close to that value (keeping in mind that the SVD decomposition by itself will only require an additional solution time comparable to one additional time point).

What are we doing here?

This post may come as a surprise to many, as ANSYS APDL is at its core a tool aiming at simulating physical phenomena so that «data reduction», being more oriented to the data analysis community, might sound a bit out-of-place.

As a matter of fact, being a numerical tool, it does have ubiquitous applications and -as we shall shortly see- it can be also beneficial to down-to-earth, goal-oriented folks like say -engineers.

Browsing the APDL Math commands, I started being curious about the *COMPRESS command, which I had so far ignored: as it was, I had assumed that it merely was a functionality aimed at compressing sparse matrices, i.e. a lossless procedure, detecting and eliminating near-zero entries. And yes, that’s exactly what it can do, but there is more to it: it will also compress data using Singular Values Decomposition (SVD), which is probably one of the most important numerical tool there is. This is not the place to provide too much background on the topic, and for those interested there is a wealth of books and articles on the subject, one prominent contribution being the online videos by Steven Brunton and Nathan Kuntz, see [1] for an introduction.

Before discussing applications, I will briefly introduce the topic of SVD, how it relates to data compression, and which APDL Math capabilities we need to use.